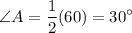1 Answer

Cecelia · Answer 1 · 2022-05-13T19:30:35+0000

Answer:

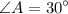
$\displaystyle \angle A=30^\circ$

Explanation:

We are given that in Circle O, Arc BAC measures 300°.

Recall that arc lengths will always total 360°. Therefore:

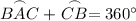
$\stackrel{\frown}{BAC}+\stackrel{\frown}{CB}=360^\circ$

By substitution:

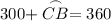
$300+\stackrel{\frown}{CB}=360$

Thus:

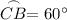
$\stackrel{\frown}{CB}=60^\circ$

∠A intercepts Arc CB. Since it is an inscribed angle, it will be half of its intercepted arc. In other words:

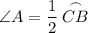
$\angle A=\displaystyle (1)/(2)\stackrel{\frown}{CB}$

Therefore:

$\displaystyle \angle A=(1)/(2)(60)=30^\circ$

Please log in or register to add a comment.