Question

What is the mass of 8.23 x 10^23 atoms of Ag

Answer 1

`\boxed {\boxed {\sf Approximately \ 147 \ g\ Ag}}`

Step-by-step explanation:

Convert Atoms to Moles

The first step is to convert atoms to moles. 1 mole of every substance has the same number of particles: 6.022 ×10²³ or Avogadro's Number. The type of particle can be different, in this case it is atoms of silver. Let's create a ratio using this information.

`(6.022*10^(23) \ atoms \ Ag)/(1 \ mol \ Ag)`

We are trying to find the mass of 8.23 ×10²³ silver atoms, so we multiply by that number.

`8.23 *10^(23) \ atoms \ Ag *(6.022*10^(23) \ atoms \ Ag)/(1 \ mol \ Ag)`

Flip the ratio so the atoms of silver cancel. The ratio is equivalent, but places the other value with units "atoms Ag" in the denominator.

`8.23 *10^(23) \ atoms \ Ag *(1 \ mol \ Ag)/(6.022*10^(23) \ atoms \ Ag)`

`8.23 *10^(23) *(1 \ mol \ Ag)/(6.022*10^(23) )`

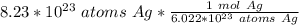
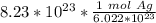
Condense into one fraction.

`(8.23 *10^(23) )/(6.022*10^(23) ) \ mol \ Ag`

`1.366655596 \ mol \ Ag`

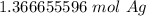
Convert Moles to Grams

The next step is to convert the moles to grams. This uses the molar mass, which is equivalent to the atomic mass on the Periodic Table, but the units are grams per mole.

• Ag: 107.868 g/mol

Let's make another ratio using this information.

`\frac {107.868 \ g \ Ag}{1 \ mol \ ag}`

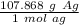
Multiply by the number of moles we calculated.

`1.366655596 \ mol \ Ag*\frac {107.868 \ g \ Ag}{1 \ mol \ ag}`

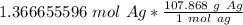
The moles of silver cancel out.

`1.366655596 *\frac {107.868 \ g \ Ag}{1 }`

`1.366655596 * {107.868 \ g \ Ag}`

`147.4184058 \ g\ Ag`

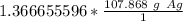
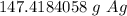
Round

The original measurement of atoms has 3 significant figures, so our answer must have the same. For the number we calculated, that is the ones place.

• 147.4184058

The 4 in the tenths place tells us to leave the 7 in the ones place.

`147 \ g\ Ag`

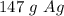
8.23 ×10²³ silver atoms are equal to approximately 147 grams.