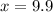Question

In the figure below,the segments JK and JL are tangent to the circle centered at O.Given that JL =13.2 and OJ=16.5,find OK.

Answer 1

OK=9.9

Explanation:

KJ and LJ both are on the circumference, are secants and coincides at the same outer point so they are equal.

JK=LJ so JK=13.2

Tangents are perpendicular to radius so the triangle in the circle is a right triangle.

Apply pythagorean theorem to find OK

`{x}^(2) + 13.2 {}^(2) = 16.5 {}^(2)`

`x = 9.9`