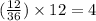Question

Simon wants to earn as many points as possible in one turn in a game. Two number cubes whose sides are numbered 1 through 6 are rolled. He is given two options for the manner in which points are awarded in the turn. OPTION A: If the sum of the rolls is a prime number, Simon receives 15 points. OPTION B: If the sum of the rolls is a multiple of 3, Simon receives 12 points. Which statement best explains the option he should choose?

Answer 1

The answer is "Option A"

Explanation:

In point A:

Rolling an indivisible prime number:

The 2 can be moved just 1 way (1,1)

The 3 can be moved two different ways (1,2) or (2,1)

The 5 can be moved four different ways (1,4) or (2,3) or (3,2) or (4,1)

The 7 can be moved six different ways (1,6) or (2,5) or (3,4) or (4,3) or (5,2) or (6,1)

The 11 can be moved two different ways (5,6) or (6,5)

There are 26 approaches to move two dice at a time.

The likelihood of rolling an indivisible number is:
`=((1 + 2 + 4 + 6 + 2))/(36) =(15)/(36)`

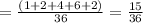
Because rolling an indivisible number is worth 15 focuses, the normal worth is
`((15)/(36)) * 15 = 6.25`

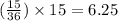
In point B:

When the rolling is a numerous of 3:

The 3 can be moved two different ways (1,2) or (2,10

The 6 can be moved five different ways (1,5) or (2,4) or (3,3) or (4,2) or (5,1)

The 9 can be moved four different ways (3,6) or (4,5) or (5,4) or (6,3)

The 12 can be moved just 1 way (6,6)

The likelihood of rolling a numerous of 3 will be:
`= ((3 + 6 + 9 + 12))/(36) = (12)/(36)`

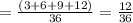
because the rolling in the various of 3 is worth 12 focuses, the normal worth is
`((12)/(36)) * 12 = 4`