Question

What is number 61 and a step by step explaination please?

Answer 1

1/3 ln(x) + ln(2) - ln(3) = 3

Recall that
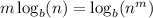`m\log_b(n)=\log_b(n^m)`, so

ln(x ¹ʹ³) + ln(2) - ln(3) = 3

Condense the left side by using sum and difference properties of logarithms:

`\log_b(m)+\log_b(n)=\log_b(mn)`

`\log_b(m)-\log_b(n)=\log_b\left(\frac mn\right)`

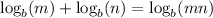
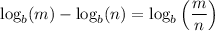
Then

ln(2/3 x ¹ʹ³) = 3

Take the exponential of both sides; that is, write both sides as powers of the constant e. (I'm using exp(x) = e ˣ so I can write it all in one line.)

exp(ln(2/3 x ¹ʹ³)) = exp(3)

Now exp(ln(x)) = x for all x, so this simplifies to

2/3 x ¹ʹ³ = exp(3)

Now solve for x. Multiply both sides by 3/2 :

3/2 × 2/3 x ¹ʹ³ = 3/2 exp(3)

x ¹ʹ³ = 3/2 exp(3)

Raise both sides to the power of 3:

(x ¹ʹ³)³ = (3/2 exp(3))³

x = 3³/2³ exp(3×3)

x = 27/8 exp(9)

which is the same as

x = 27/8 e ⁹