Two decimals numbers, to the thousandths, that have a sum of about 5 and a difference of about 3. Then do the math to prove it works.

Question

asked Jan 9, 2022 6.0k views

1 Answer

David Dollar · Answer 1 · 2022-01-14T11:54:38+0000

Answer:

The numbers are approximately: 4.000 and 1.000

Explanation:

The given parameters can be expressed as:

$(x)/(1000) + (y)/(1000) \approx 5$

$(x)/(1000) - (y)/(1000) \approx 3$

Required

Determine the numbers

In each of the equations, multiply by 1000

$1000 * [(x)/(1000) + (y)/(1000) \approx 5]$

$x + y \approx 5000$

$1000 * [(x)/(1000) - (y)/(1000) \approx 3]$

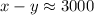
$x-y \approx 3000$

So, we have:

$x + y \approx 5000$

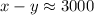
$x-y \approx 3000$

Add the two equations

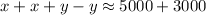
$x + x + y - y \approx 5000 + 3000$

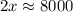
$2x \approx 8000$

Solve for x

$x \approx 8000/2$

$x \approx 4000$

Substitute
$x \approx 4000$ in
$x + y \approx 5000$

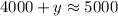
$4000 + y \approx 5000$

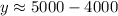
$y \approx 5000 - 4000$

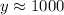
$y \approx 1000$

Using:

$(x)/(1000) + (y)/(1000) \approx 5$

We have:

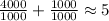
$(4000)/(1000) + (1000)/(1000) \approx 5$

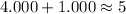
$4.000 + 1.000 \approx5$

This implies that, the numbers approximates to 4.000 and 1.000, respectively.