Question

The upper-left coordinates on a rectangle are (-6,0)(−6,0)left parenthesis, minus, 6, comma, 0, right parenthesis, and the upper-right coordinates are (-4,0)(−4,0)left parenthesis, minus, 4, comma, 0, right parenthesis. The rectangle has an area of 121212 square units. Draw the rectangle on the coordinate plane below.

Answer 1

See attachment for rectangle

Explanation:

Given

`A = (-6,0)`

`B = (-4,0)`

`Area = 12`

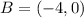
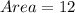
Required

Draw the rectangle

First, we calculate the distance between A and B using distance formula;

`AB = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

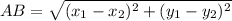
So, we have:

`AB = √((-6 - -4)^2 + (0- 0)^2)`

`AB = √((-2)^2 + (0)^2)`

`AB = √(4 + 0)`

`AB = √(4)`

`AB = 2`

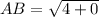
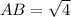
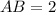
The above represents the length of the triangle.

Next, calculate the width using:

`Length * Width = Area`

`2* Width = 12`

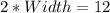
Divide both sides by 2

`Width = 6`

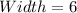
This implies that, the width of the rectangle is 6 units.

We have:

`A = (-6,0)`

`B = (-4,0)`

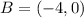
Since A and B are at the upper left and right, then the ther two points are below.

6 units below each of the above point are:

`C = (-6,0-6)\\` =>
`C = (-6,-6)`

`D = (-4,0-6)` =>
`D = (-4,-6)`

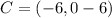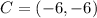
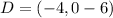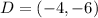
Hence, the points of the rectangle are:

`A = (-6,0)`

`B = (-4,0)`

`C = (-6,-6)`

`D = (-4,-6)`

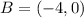
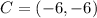
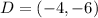
See attachment for rectangle