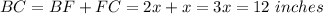Answer:
The answer is "12 inches".
Explanation:
Please find the image file of the graph.
We know
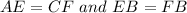 so because the triangle is isosceles.
so because the triangle is isosceles.
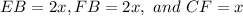 when
when
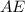 is called by
is called by
 .
.
We know that
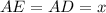 since E and D are tangent points to a circle.
since E and D are tangent points to a circle.
They have
 since D and F are tangent points only to circle.
since D and F are tangent points only to circle.
Thus, if the perimeter is 32, the following is the result:
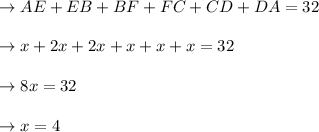
Therefore the length of