Question

In a shear box test on sand a shearing force of 800 psf was applied with normal stress of 1750 psf. Find the major and minor principal stresses.

Answer 1

The major and minor stresses are as 2060.59 psf, -310.59 psf and 1185.59 psf.

Step-by-step explanation:

The major and minor principal stresses are given as follows:

`\sigma_(max)=(\sigma_x+\sigma_y)/(2)+\sqrt{\left((\sigma_x-\sigma_y)/(2)\right)^2+\tau_(xy)^2}`

`\sigma_(min)=(\sigma_x+\sigma_y)/(2)-\sqrt{\left((\sigma_x-\sigma_y)/(2)\right)^2+\tau_(xy)^2}`

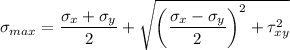
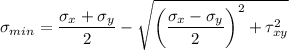
Here

• 
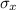  `\sigma_x` is the normal stress which is 1750 psf
• 
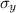  `\sigma_y` is 0
• 
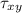  `\tau_(xy)` is the shear stress which is 800 psf

So the formula becomes

Similarly, the minimum normal stress is given as

`\sigma_(min)=(\sigma_x+\sigma_y)/(2)-\sqrt{\left((\sigma_x-\sigma_y)/(2)\right)^2+\tau_(xy)^2}\\\sigma_(min)=(1700+0)/(2)-\sqrt{\left((1700-0)/(2)\right)^2+(800)^2}\\\sigma_(min)=875-√((875)^2+(800)^2)\\\sigma_(min)=875-√(765625+640000)\\\sigma_(min)=875-1185.59\\\sigma_(min)=-310.59 \text{ psf}`

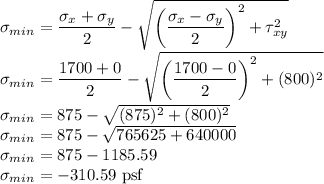
The maximum shear stress is given as

`\tau_(max)=(\sigma_(max)-\sigma_(min))/(2)\\\tau_(max)=(2060.59-(-310.59))/(2)\\\tau_(max)=(2371.18)/(2)\\\tau_(max)=1185.59 \text{psf}`