Question

The accompanying table shows the number of bacteria present in a certain culture over a 4 hour period, where x is the time, in hours, and y is the number of bacteria.Write an exponential regression equation for this set of data, rounding all coefficients to the nearest thousandth. Using this equation, determine the number of bacteria present after 11 hours, to the nearest whole number.

Answer 1

Answer: 7041 is the answer. I’m not sure how to explain. I took a lucky guess on my quizzez assignment and got it correct.

Answer 2

The exponential regression equation, rounded to the nearest hundredth, is: y = 464 *
`(1.08)^x`

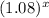
The estimated number of bacteria present after 11 hours is approximately 1082

How to find the exponential regression equation

To find the exponential regression equation for the given set of data, use the formula for exponential growth:

`y = ab^x`

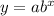
Where:

y is the number of bacteria

x is the time in hours

a is the initial value or the number of bacteria at x=0

b is the growth factor or the rate of growth

Let's use the given data points to find the values of a and b.

For x = 0: y = 464 = a *
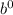`b^0` = a (since any number raised to the power of 0 is 1)

So, a = 464.

Now, use another data point to find the value of b.

Let's use x = 1:

For x = 1: y = 500

500 = a *
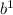`b^1` = 464 * b

500 = 464b

So, b = 500 / 464 ≈ 1.08 (rounded to two decimal places).

Therefore, the exponential regression equation, rounded to the nearest hundredth, is:

y = 464 *
`(1.08)^x`

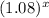
To determine the number of bacteria present after 11 hours,

substitute x = 11 into the equation:

y = 464 *
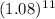`(1.08)^1^1` ≈ 1081.88

Rounding to the nearest whole number, the estimated number of bacteria present after 11 hours is approximately 1082

The accompanying table shows the number of bacteria present in a certain culture over a 4 hour period, where x is the time, in hours, and y is the number of bacteria. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, determine the number of bacteria present after 11 hours, to the nearest whole number.

Hours (x): 0, 1, 2, 3, 4

Bacteria (y): 464, 500, 561, 632, 678