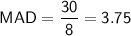Question

Please please please help

find the median

72 82 92 93 94 97 98 102


find the median

53 59 64 65 65 66 67 69

find the mean absolute deviation (MAD)

72
82
93
98
102
97
92
94

find the mean absolute deviation (MAD)

53 59 64 65 65 66 67 69

Answer 1

median = 93.5

median = 65

MAD = 7.125

MAD = 3.75

Explanation:

The median is the middle value when the values of the data set are placed in order from smallest to largest.

Data set: 72 82 92 93 94 97 98 102

As the number of values in the data set is even, the median is the mean of the middle two values.

`\implies \sf median=(93+94)/(2)=93.5`

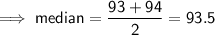
Data set: 53 59 64 65 65 66 67 69

As the number of values in the data set is even, the median is the mean of the middle two values.

`\implies \sf median=(65+65)/(2)=65`

To find the Mean Absolute Deviation (MAD):

1. calculate the mean (by summing the data values and dividing by the number of values)

2. Subtract the mean from each value in the data set and take the absolute value of each result.

3. Sum the absolute values from step 2.

4. Divide by the number of values.

Data set: 72, 82, 93, 98, 102, 97, 92, 94

`\sf Mean=(72+82+93+98+102+97+92+94)/(8)=91.25`

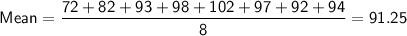
|72 - 91.25| = 19.25

|82 - 91.25| = 9.25

|93 - 91.25| = 1.75

|98 - 91.25| = 6.75

|102 - 91.25| = 10.75

|97 - 91.25| = 5.75

|92 - 91.25| = 0.75

|94 - 91.25| = 2.75

Sum of absolute values = 57

`\sf MAD=(57)/(8)=7.125`

Data set: 53 59 64 65 65 66 67 69

`\sf Mean=(53 +59+ 64+ 65+ 65+ 66+ 67+ 69)/(8)=63.5`

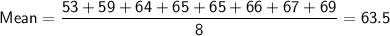
|53 - 63.5| = 10.5

|59 - 63.5| = 4.5

|64 - 63.5| = 0.5

|65 - 63.5| = 1.5

|65 - 63.5| = 1.5

|66 - 63.5| = 2.5

|67 - 63.5| = 3.5

|69 - 63.5| = 5.5

Sum of absolute values = 30

`\sf MAD=(30)/(8)=3.75`