Question

What is the likelihood that a point chosen inside the square will also be inside the circle ?It Chose one : A. is impossible ,B. it is unlikely, C it is likely D. it is certain

Answer 1

C. Likely

Explanation:

all the points are in the circle so it's likely to choose a point inside the circle

Answer 2

C. It is likely

Explanation:

Given

See attachment for diagram

For the square.

Let

`Length = L`

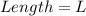
So, the area is:

`Area = Length^2`

`A_1=L^2`

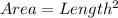
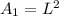
The side length of the square equals the diameter of the circle.

So:

`diameter (d) = L`

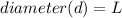
The radius is:

`r = (1)/(2)d`

`r = (1)/(2)L`

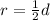
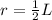
The area is:

`Area = \pi r^2`

`A_2 = \pi * ((1)/(2)L)^2`

`A_2 = \pi * (1)/(4)L^2`

`A_2 = (22)/(7) * (1)/(4)L^2`

`A_2 = (22)/(28) L^2`

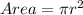
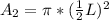
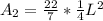
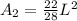
The likelihood that a point will be common to the square and the circle is:

`Pr = (A_2)/(A_1)`

`Pr = ((22)/(28) L^2)/(L^2)`

`Pr = (22)/(28)`

`Pr = 78.57\%`

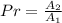
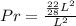
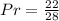
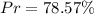
The above probability is greater than 50% but less than 100%.

Hence, it is likely