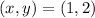Question

How do you solve 2x-3y=-4 and x=7-3y by substitution?

Answer 1

`(1, 2)`

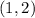
Explanation:

We can solve this system using substitution.

In this case, we can substitute 7-3y for x, as they are of equal value.

Therefore...

`2x-3y=-4\\2(7-3y)-3y=-4\\14-6y-3y=-4\\14-9y=-4`

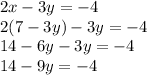
Subtract 14 from both sides:

`-9y=-18`

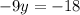
Divide both sides by -9

`y=2`

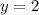
Now, substitute 2 for y to solve for x:

`x=7-3y=7-3(2)=7-6=1`

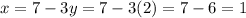
Therefore the solution to this system of equations is:

`(x, y)=(1, 2)`