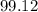 is the answer.
is the answer.
Step-by-step Explanation:
To find- Probability area bound by 93% or 0.93.
Steps-
0.5 lies to the lie of the mean value.
→ 0.93 - 0.5 = 0.43 lies to the right of the mean.
Now find the corresponding "z" value for 0.43
It is 1.48.
Use this value to determine the requix value.
You have to use the formula -
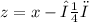
Solve it for
 :-
:-
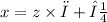
Where;

Now put these values in the
formula;
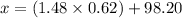

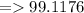
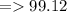
Hence, the temperature that separates
top 7% from the bottom 93%
is 99.12.