Question

The cost of 7 chairs and 2 tables is equal.If the cost of 6 chairs and 5 tables is 10575, find the cost of 12 chairs.​

Answer 1

5400

Explanation:

Let x represent the cost of a chair and y represent the cost of a table. We can use this to set up a system of equations:

7x=2y

6x+5y=10575

We can solve this system using substitution.

Start by rewriting the first equation in terms of x.

`7x=2y\\\text{Divide both sides by 7}\\x=(2)/(7)y`

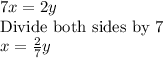
Substitute this into the second equation:

`6((2)/(7)y)+5y=10575\\(12)/(7)y+5y+10575\\(12)/(7)y+(35)/(7)y=10575\\(47)/(7)y=10575`

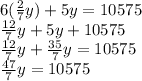
Multiply both sides by 7

`47y=74025`

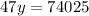
Divide both sides by 47

`y=1575`

This means...

`7x=2(1575)\\7x=3150`

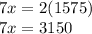
Divide both sides by 7

`x=450`

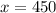
One chair costs 450. Now, multiply this number by 12 to find the cost of 12 chairs.

`450*12=5400`

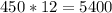
12 chairs cost 5400.