Given:
The sides of each brace have lengths 63 feet, 46 feet, and 40 feet.
To find:
The measure of the angle opposite the 46 foot side.
Solution:
According to the Law of Cosines:
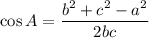
We need to find the measure of the angle opposite the 46 foot side. So,
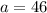 and the other sides are
and the other sides are
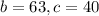 .
.
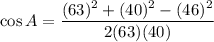
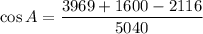
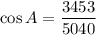
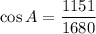
Taking cos inverse on both sides, we get
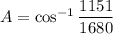
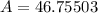
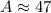
Therefore, the measure of the angle opposite the 46 foot side is 47 degrees.