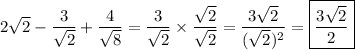Question

Simplify and express


`2 √(2) - (3)/( √(2) ) + (4)/( √(8) )`
as a single surd​

Answer 1

First a few reminders:

• For a ≠ 0 and b ≥ 0,
`\sqrt[a]{b}=b^(\frac1a)`

• 4 = 2² and 8 = 2³

• For real numbers a, b, c, we have
`(a^b)^c=a^(bc)`

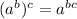
• For any real numbers a and n (so long as both are not zero), we have
`\frac1{a^n}=a^(-n)`

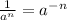
• For any numbers a, b, c,
`a^b* a^c=a^(b+c)`

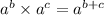
So we have

`\sqrt2=2^(\frac12)`

`\frac1{\sqrt2}=2^(-\frac12)`

`\frac1{\sqrt8}=\frac1{(2^3)^(\frac12)}=2^(-\frac32)`

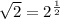
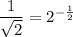
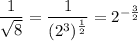
Then the given expression can be rewritten as

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=2*2^(\frac12)-3*2^(-\frac12)+2^2*2^(-\frac32)`

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=2^(1+\frac12)-3*2^(-\frac12)+2^(2-\frac32)`

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=2^(\frac32)-3*2^(-\frac12)+2^(\frac12)`

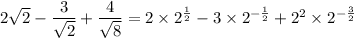
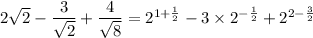
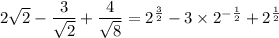
Pull out a factor of
`2^(-\frac12)`:

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=2^(-\frac12)\left(2^(\frac32+\frac12)-3+2^(\frac12+\frac12)\right)`

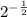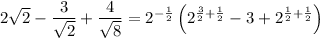
Simplify this:

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=2^(-\frac12)\left(2^2-3+2^1\right)=2^(-\frac12)(4-3+2)=3*2^(-\frac12)=\frac3{\sqrt2}`

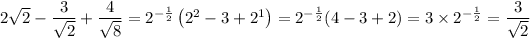
Rationalize this last result to get the square root out of the denominator:

`2\sqrt2-\frac3{\sqrt2}+\frac4{\sqrt8}=\frac3{\sqrt2}*(\sqrt2)/(\sqrt2)=(3\sqrt2)/((\sqrt2)^2)=\boxed{\frac{3\sqrt2}2}`