Answer:
Part A:
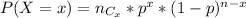
x is a binomial Random Variable.
Part B:
Value of p=0.8
Value of n=20
Part C:
P(X=15)=0.17456
Part D:
P(X≥15)=0.80417
Part E:
E(x)=16
E(x) tells us that out of 20 tracks the SBIRS will detect from 16 tracks.
Explanation:
Part A:
Binomial Distribution is used because the number of tracks and the probability to find the intruding object is constant for all tracks
It means:
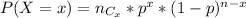
x is a binomial Random Variable.
Part B:
Value of p=0.8
Value of n=20
Part C:
x=15
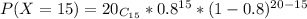
By solving above Expression:
P(X=15)=0.17456
Part D:
P(X≥15)=P(X=15)+P(X=17)+P(X=16)+P(X=18)+P(X=19)+P(X=20)
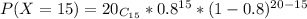
P(X=15)=0.17456
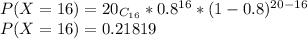
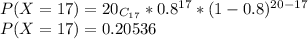
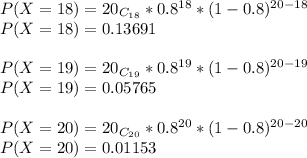
Now, Adding Probabilities:
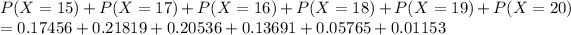
P(X≥15)=0.80417
Part E:
Mean Distribution:
E(x)=n*p
E(x)=20*0.8
E(x)=16
E(x) tells us that out of 20 tracks the SBIRS will detect from 16 tracks.