Question

According to a report in USA Today (February 1, 2012), more and more parents are helping their young adult children get homes. Suppose 8 persons in a random sample of 40 young adults who recently purchased a home in Kentucky got help from their parents. You have been asked to construct a 95% confidence interval for the population proportion of all young adults in Kentucky who got help from their parents. You have been asked to construct a 95% confidence interval for the population proportion of all young adults in Kentucky who got help from their parents. What is the margin of error for a 95% confidence interval for the population proportion?

a.1.645(0.0040)
b.1.645(0.0632)
c.1.96(0.0040)
d.1.96(0.0632)

Answer 1

d.1.96(0.0632)

Explanation:

The margin of error for a 95% confidence interval for the population proportion calculated as below:

Given that x = 8

n = Size of the sample = 40 (Large sample)

Sample population: P=x/n = 8/40 = 0.2; q = 1-p = 0.8

Standard error =
`√(pq/n)` =
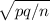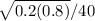`√(0.2(0.8))/40` = 0.0682

95% of confidence Z∝ = 1.96

Margin of Error = Z∝ .
`√(pq/n)`

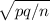
Margin of Error = 1.96(0.0682)

So, therefore, option d is correct.