Question

An investor wants to invest up to $100,000 as follows:

X amount into a Certificate of Deposit (CD) that yields an expected annual return of 1% with a risk index of 1,
Y amount into a Bond with an expected annual return of 3% and a risk index of 4,
Z amount into a Stock with an expected annual return of 7% and a risk index of 8.
The investor’s objective is to maximize the total expected annual return of the investment.

However, to be prudent, the investor requires that:
The fraction of the total investment in X must be at least 20%.
The fraction of the total investment in Z must not exceed 50%.
The combined portfolio risk index must not exceed 5.

Required:
a. Set up this investment problem as a linear program, which has 3 variables, 3 basic constraints, and 4 special constraints.
b. Use an LP software to find the maximum expected annual return in dollars and the dollar values of X, Y, and Z for this best investment.
c. From the software solution, show the values of the dual variables for the four special constraints.

Answer 1

a-The Linear Model is as follows:

`X+Y+Z\leq 100,000\\{0.001X}\geq 20\\{0.001Z}\leq 50\\0.00001X+0.00004Y+0.00008Z\leq5\\X\geq0\\Y\geq0\\Z\geq0`

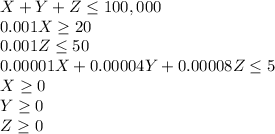
b-The values are

X=$33,333.33

Y=$16,666.67

Z=$50,000.00

Leading to a total expected return of $4333.33.

c-The values of constraints are as follows

X+Y+Z=33333.33+16666.67+50000=100,000

X=33%, Y is 16.67% and Z is 50%

Risk component of X is 0.33

Risk component of Y is 0.66

Risk component of Z is 4.00

Explanation:

a

From the conditions, the first special constraint is the total amount which is that the sum of investments must not be more than the total available amount of $100,000 so

`X+Y+Z\leq 100,000`

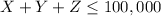
The second special constraint is that the percentage of X must be at least 20% So

`(X)/(100,000)*100 \geq20\\(X)/(1000) \geq20\\{0.001X}\geq 20`

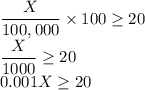
The third special constraint is that the fraction of total investment of Z must not exceed 50% So

`(Z)/(100,000)*100 \leq50\\(Z)/(1000)\leq 50\\0.001Z\leq50`

The fourth special constraint is that the combined portfolio risk index must not exceed 5 so

`(X)/(100,000)*1+(Y)/(100,000)*4+(Z)/(100,000)*8\leq5\\0.00001X+0.00004X+0.00008Z\leq5`

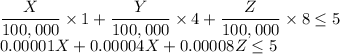
As the investments cannot be negative so three basic constraints are

`X\geq0\\Y\geq0\\Z\geq0`

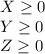
The maximization function is given as

`f(X,Y,Z)=(X)/(X+Y+Z)*1\%+(Y)/(X+Y+Z)*3\%+(Z)/(X+Y+Z)*7\%\\f(X,Y,Z)=(X)/(X+Y+Z)*0.01+(Y)/(X+Y+Z)*0.03+(Z)/(X+Y+Z)*0.07`

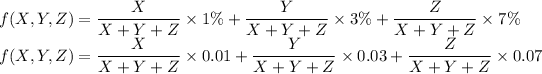
b

By using an LP solver with BigM method the solution is as follows:

X=$33,333.33

Y=$16,666.67

Z=$50,000.00

Leading to a total expected return of $4333.33.

c

The values of constraints are as follows

X+Y+Z=33333.33+16666.67+50000=100,000

X=33%, Y is 16.67% and Z is 50%

Risk component of X is 0.33

Risk component of Y is 0.66

Risk component of Z is 4.00