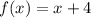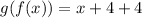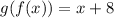Answer:
(a) and (b)
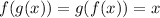
(c) and (d)
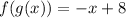
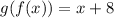
Explanation:
Given
(a) to (d)
Required
Find f(g(x)) and g(f(x)) for each pair
For (a) and (b), we have:
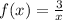
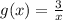
Calculate f(g(x))
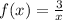
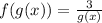
Substitute 3/x for g(x)
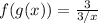
Rewrite as:
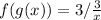
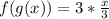
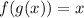
Since f(x) = g(x), then:
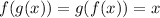
For (c) and (d)
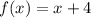
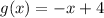
Solving f(g(x)), we have:
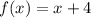
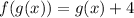
Substitute
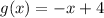
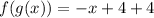
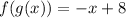
Calculating g(f(x))
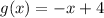
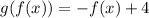
Substitute: