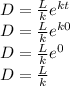Question

Litter such as leaves falls to the forest floor, where the action of insects and bacteria initiates the decay process. Let A be the amount of litter present, in grams per square meter, as a function of time t in years. If the litter falls at a constant rate of L grams per square meter per year, and if it decays at a constant proportional rate of k per year, then the limiting value of A is R = L/k. For this exercise and the next, we suppose that at time t = 0, the forest floor is clear of litter.

Required:
If D is the difference between the limiting value and A, so that D = R - A, then D is an exponential function of time. Find the initial value of D in terms of R.

Answer 1

D = L/k

Explanation:

Since A represents the amount of litter present in grams per square meter as a function of time in years, the net rate of litter present is

dA/dt = in flow - out flow

Since litter falls at a constant rate of L grams per square meter per year, in flow = L

Since litter decays at a constant proportional rate of k per year, the total amount of litter decay per square meter per year is A × k = Ak = out flow

So,

dA/dt = in flow - out flow

dA/dt = L - Ak

Separating the variables, we have

dA/(L - Ak) = dt

Integrating, we have

∫-kdA/-k(L - Ak) = ∫dt

1/k∫-kdA/(L - Ak) = ∫dt

1/k㏑(L - Ak) = t + C

㏑(L - Ak) = kt + kC

㏑(L - Ak) = kt + C' (C' = kC)

taking exponents of both sides, we have

`L - Ak = e^(kt + C') \\L - Ak = e^(kt)e^(C')\\L - Ak = C`

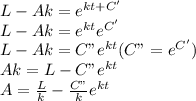
When t = 0, A(0) = 0 (since the forest floor is initially clear)

`A = (L)/(k) - (C`

`A = (L)/(k) - (L)/(k) e^(kt)`

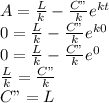
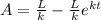
So, D = R - A =

`D = (L)/(k) - (L)/(k) - (L)/(k) e^(kt)\\D = (L)/(k) e^(kt)`

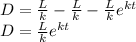
when t = 0(at initial time), the initial value of D =

`D = (L)/(k) e^(kt)\\D = (L)/(k) e^(k0)\\D = (L)/(k) e^(0)\\D = (L)/(k)`