Question

You are managing a city that needs to upgrade its disinfection basin at your 40 MGD surface water drinking water treatment plant. You would like to use chlorine (Cl2) as your disinfectant and you need to achieve a 4-log removal of E. coli. You are deciding between a traditional 750,000 gallon PFR contact basin (serpentine flow) and a newer system which contains three 150,000 gallon CSTRs in series, each receiving an equal injection of Cl2. Your final decision is going to be based on which system requires the least amount of Cl2 to achieve a 4-log removal of E. coli.

Required:
What is the amount of Cl2 required to operate each system (please answer in units of kg Cl/day)?

Answer 1

According to Chick's law

`$(N_t)/(N_0)=e^(-k'C^n t)$`

where, t = contact time

c = concentration of disinfectant

k' = lethality coefficient = 4.71

n = dilution coefficient = 1

4 log removal = % removal = 99.99

`$(N_t)/(N_0)=\frac{\text{bacteria remaining}}{\text{bacteria initailly present}}$`

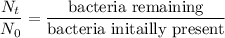
= 1 - R

= 1 - 0.9999

Now for plug flow reactor contact time,

`$\tau =(V)/(Q) =(75000)/(40 * 10^6)$`

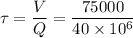
= 0.01875 days

= 27 minutes

For CSTR,
`$\tau =(V)/(Q) =(150000)/(40 * 10^6)$`

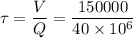
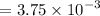`$=3.75 * 10^(-3)$` days

= 5.4 minute

There are 3 reactors, hence total contact time = 3 x 5.4

= 16.2 minute

Or
`$(N_t)/(N_0)=e^(-k'C^n t)$`

or
`$(1-0.9999)=e^(-4.71 * C * t)$`

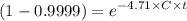
∴ C x t = 1.955

For PFR,
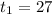`$t_1 = 27 $` min

∴ C
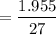`$=(1.955)/(27)$` = 0.072 mg/L

For CSIR,
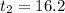`$t_2=16.2$` min

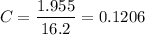`$C=(1.955)/(16.2) = 0.1206$` mg/L

∴ Chlorine required for PFR in kg/day

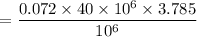`$=(0.072 * 40 * 10^6 * 3.785)/(10^6)$` (1 gallon = 3.785 L)

= 18.25 kg/day

Therefore we should go for PFR system.