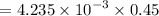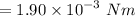Question

A 700-gram grinding wheel 22.0 cm in diameter is in the shape of a uniform solid disk. (We can ignore the small hole at the center.) When it is in use, it turns at a constant 215 rpm about an axle perpendicular to its face through its center. When the power switch is turned off, you observe that the wheel stops in 50.0 s with constant angular acceleration due to friction at the axle.

What torque does friction exert while this wheel is slowing down?

Answer 1

Given :

Mass of grinding wheel, m = 700 g

= 0.7 kg

Diameter of the grinding wheel, d = 22 cm

= 0.22 m

Radius of the grinding wheel, r = 0.11 m

Initial angular velocity of grinding wheel,
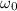`$\omega_0$` = 215 rpm

`$=215 \ rpm * (2 \pi \ rad)/(1 \ rev)* (1 \ min)/(60 \ s)$`

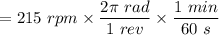
where,
`$\pi = (22)/(7)$`

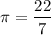
Time taken to stop, t = 50 s

Final angular velocity is
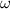`$\omega$` = 0

Angular acceleration of the grinding wheel is given by :

`$\alpha = (\omega-\omega_0)/(t)$`

`$=(0-215 \ rpm * (2 \pi \ rad)/(1 \ rev)* (1 \ min)/(60 \ s))/(50 \ s)$`

`$=-0.45 \ rad/s^2$`

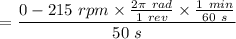
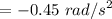
Magnitude of the angular acceleration of grinding wheel
`$\alpha$`
`$=-0.45 \ rad/s^2$`

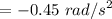
Moment of inertia of the grinding wheel (solid disk),

`$I=(1)/(2)mR^2$`

`$=(1)/(2) * 0.7 * 0.11^2$`

`$=4.235 * 10^(-3) \ kgm^2$`

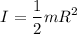
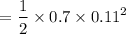
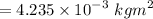
Torque exerted by friction while the wheel is slowing down is

`$\tau = I \alpha$`

`$=4.235 * 10^(-3) * 0.45$`

`$=1.90 * 10^(-3) \ Nm$`