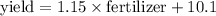Question

A farmer wants to know the effect of using various amounts of fertilizer in relation to the yield of his crops. Be subdivided a portion of his land into 10 separate but essentially equal plots. He divided the land so that all of the plots had equal exposure to sun, rain, and other environmental conditions. He randomly selected 2 of the 10 plots and spread 2 pounds of fertilizer over each of them. Then he randomly selected 2 of the remaining plots and spread 3 pounds of fertilizer over each of them. He continued with the last sets of plots in the same manner, spreading 4, then 5, then 6 pounds of fertilizer over each of them. Below is a computer output for linear regression of amount of fertilizer versus yield for the 10 plots of land.

Predictor Coef SE Coef T P
Constant 10.100 0.7973 12.67 0.000
Fertiz 1.150 0.1879 6.12 0.000

Required:
What is the equation of the least squares regression line from this sample?

Answer 1

The equation of line is

`\text{yield}=1.15* \text{fertilizer}+10.1`

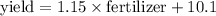
Explanation:

The general equation of line is given as

`y=mx+b`

where

y is the dependent variable which is yield in this case.

x is the independent variable which is fertilizer in this case

m is the coefficient of the fertilizer whose value is 1.150 from the given values.

b is the constant whole value is 10.100 from the given values.

Thus the equation becomes.

`\text{yield}=1.15* \text{fertilizer}+10.1`