Question

A major traffic problem in the Greater Cincinnati area involves traffic attempting to cross the Ohio River from Cincinnati to Kentucky using Interstate 75. Let us assume that the probability of no traffic delay in one period, given no traffic delay in the preceding period, is 0.85 and that the probability of finding a traffic delay in one period, given a delay in the preceding period, is 0.75. Traffic is classified as having either a delay or a no-delay state, and the period considered is 30 minutes.

a. Assume that you are a motorist entering the traffic system and receive a radio report of a traffic delay. What is the probability that for the next 60 minutes (two time periods) the system will be in the delay state? Note that this result is the probability of being in the delay state for two consecutive periods. If required, round your answer to three decimal places.
b. What is the probability that in the long run the traffic will not be in the delay state? If required, round your answers to three decimal places.

Answer 1

a. 0.563 = 56.3% probability that for the next 60 minutes (two time periods) the system will be in the delay state.

b. 0.625 = 62.5% probability that in the long run the traffic will not be in the delay state

Explanation:

Question a:

The probability of finding a traffic delay in one period, given a delay in the preceding period, is 0.75.

The system currently is in traffic delay, so for the next time period, 0.75 probability of a traffic delay. If the next period is in a traffic delay, the following period will also have a 0.75 probability of a traffic delay. So

0.75*0.75 = 0.563

0.563 = 56.3% probability that for the next 60 minutes (two time periods) the system will be in the delay state.

b. What is the probability that in the long run the traffic will not be in the delay state? If required, round your answers to three decimal places.

If it doesn't have a delay, 85% probability of continuing without a delay.

If it has a delay, 75% probability of continuing with a delay.

So, for the long run:

x: current state

85% probability of no delay if x is in no delay, 100 - 75 = 25% if x is in delay(1-x). So

`0.85x + 0.25(1 - x) = x`

`0.6x + 0.25 = x`

`0.4x = 0.25`

`x = (0.25)/(0.4)`

`x = 0.625`

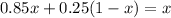
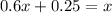
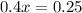
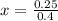
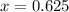
0.625 = 62.5% probability that in the long run the traffic will not be in the delay state