Question

A 2:2 kg toy train is con ned to roll along a straight, frictionless track parallel to the x-axis. The train starts at the origin moving at a speed of 1:6m=s in the +x direction, and continues until it reaches a position 7:5m down the track from where it started. During its journey, it experiences a force pointing in the same direction as the vector 0:6 +0:8 , with magnitude initially 2:8N and decreasing linearly with its x-position to 0N when the train has finished its journey.

Required:
a. Calculate the work done by this force over the entire journey of the train.
b. Find the speed of the train at the end of its journey.

Answer 1

a) 10.51 J

b) 3.48 m/s

Step-by-step explanation:

Given data :

mass of train ( M ) = 2.2 kg

Given initial velocity ( u ) = 1.6 m/s

a) calculating work done by the force over the journey of the train

F = mx + b ------ ( 1 )

m = slope = ( Δ f / Δ x ) = 2.8 / -7.5 = - 0.373 N/m

x = distance travelled on the x axis by the train = 7.5 m

F = force experienced by the train = 2.8 N

x = 0

∴ b = 2.8

hence equation 1 can be written as

F = ( -0.373) x + 2.8 ----- ( 2 )

hence to determine the work done by the force

W =
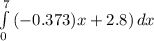`\int\limits^7_0 { ( -0.373) x + 2.8 )} \, dx` Note: the limits are actually 7.5 and 0

∴ W ( work done ) = -10.49 + 21 = 10.51 J

b) calculate the speed of the train at the end of its journey

we will apply the work energy theorem

W = 1/2 m*v^2 - 1/2 m*u^2

∴ V^2 = 2 / M ( W + 1/2 M*u^2 ) ( input values into equation )

V^2 = 12.11

hence V = 3.48 m/s