Question

It has been reported that 8.7% of U.S. households do not own a vehicle, with 33.1% owning 1 vehicle, 38.1% owning 2 vehicles, and 20.1% owning 3 or more vehicles. The data for a random sample of 100 households in a resort community are summarized in the frequency distribution below. At the 0.05 level of significance, can we reject the possibility that the vehicle-ownership distribution in this community differs from that of the nation as a whole?

Number of Vehicles Owned Number of Households 0 20 1 35 2 23 3 or more 22 =100

Answer 1

To determine if the vehicle-ownership distribution in the resort community differs from that of the nation, we need to perform a hypothesis test using the chi-square test statistic.

Step-by-step explanation:

To determine if the vehicle-ownership distribution in the resort community differs from that of the nation, we need to perform a hypothesis test. We can set up the null hypothesis as the vehicle-ownership distribution in the community is the same as the nation's distribution and the alternative hypothesis as the two distributions are different.

Next, we need to calculate the expected frequencies for each category in the sample based on the proportions in the nation. We can then use the chi-square test statistic to compare the observed and expected frequencies. If the chi-square test statistic exceeds the critical value at the 0.05 significance level, we can reject the null hypothesis and conclude that the vehicle-ownership distribution in the community differs from that of the nation.

Answer 2

Here, the test statistics ( 20.951 ) is greater than the critical value ( 7.815 )

Therefore, we reject H₀ at 0.05 level of significance.

Hence, there is significant evidence to support the claim that In this community, vehicle ownership distribution is NOT like that of all U.S household

Step-by-step explanation:

Given the data in the question;

Number of vehicle owned Number of households

0 20

1 35

2 23

3 or more 22

Total ( n ) 100

so

Null hypothesis H₀ : In this community, vehicle ownership distribution is like that of all U.S household

Alternative hypothesis Hₐ : In this community, vehicle ownership distribution is NOT like that of all U.S household

Also given that, ∝ = 0.05

Now, we compute the test statistics;

x² = ∑[ ( O
`_i` - E
`_i` ) / E
`_i` ]

where E
`_i` is expected frequency and O
`_i` is observed frequency.

so we make our table for chi square test statistics

No. of O
`_i` P E
`_i` (O
`_i` - E
`_i`)² (O
`_i` - E
`_i`)²/E
`_i`

Vehicle (n×P)

owned

0 20 0.087 8.7 127.69 14.677

1 35 0.331 33.1 3.61 0.109

2 23 0.381 38.1 228.01 5.985

3 or more 22 0.201 20.1 3.61 0.180

Total 100 100 20.951

hence, x² = 20.951

Now, degree of freedom df = k - 1 = 4 - 1 = 3

From Chi-Square critical value table; ( right tailed test ) for ∝ = 0.05

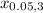`x_{0.05, 3` = 7.815

Decision Rule

Reject H₀ if x² is greater than xₐ².

Here, the test statistics ( 20.951 ) is greater than the critical value ( 7.815 )

Therefore, we reject H₀ at 0.05 level of significance.

Hence, there is significant evidence to support the claim that In this community, vehicle ownership distribution is NOT like that of all U.S household