Answer:
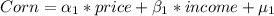 --- Demand
--- Demand
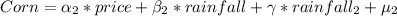 --- Supply
--- Supply
Explanation:
Given
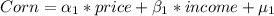
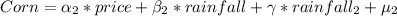
Required
Identify the demand and the supply equation.
To identify which is the demand equation and which is the supply equation, we simply look through the constraints of the equation.
For (1):
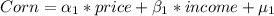
We have: Price and Income
For (2):
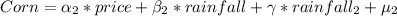
We have: Price and Rainfall
In (1), price and income determines the demand of a product.
Hence, (1) represents the demand equation
In (2), price and weather condition (rainfall) determines the supply of a product.
Hence, (2) represents the supply equation.