Answer:
the correct result is L = 0.319 m
Step-by-step explanation:
This system is a physical pendulum whose angular velocity is
w² =
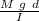
where d is the distance from the center of mass to the point of rotation and I is the moment of inertia of the system
The Moment of Inertia is a scalar, therefore an additive quantity
I = I_bar + I_disk
the moment of inertia of each element with respect to the pivot point can be found with the parallel axes theorem
let's use M for the mass of the bar and m for the mass of the disk
Bar
I_bar = I_{cm} + Md²
the moment of inertia of the center of mass is
I_{cm} =
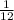 M L²
M L²
the distance from the center of mass
d = L / 2
we substitute
I_bar =
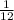 M L² + M (
M L² + M (
 )
)
Disk
I_disk = I_{cm} + m d²
moment of inertia of the center of mass
I_{cm} = ½ m R²
the distance d is
d = L
we substitute
I_disk = 1/2 m R² + m L²
the total moment of inertia is
I =
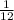 M L² +
M L² +
 M L² +
M L² +
 m r² + m L²
m r² + m L²
I =
 M L² + m L² + ½ m r²
M L² + m L² + ½ m r²
I = L² (m +
 M) + ½ m r²
M) + ½ m r²
The position of the center of mass of the system can be found with the expressions
d_{cm} =
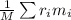
d_{cm} =
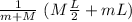
d_{cm} =
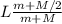
now we can substitute in the expression for the angular velocity
w² = (m + M) g L
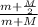
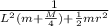
w² = g (m +
 M)
M)
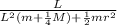
angular velocity and period are related
w = 2π/T
sustitute
4π²/T² = g (m +
 M)
M)
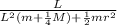
L² (m +
 M) + ½ m r² =
M) + ½ m r² =
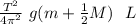
we substitute the values and solve the second grade equation
L² (0.1 +
 0.3) - [
0.3) - [
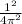 9.8 (0.1 + 0.3/2) ] L + ½ 0.1 0.2² = 0
9.8 (0.1 + 0.3/2) ] L + ½ 0.1 0.2² = 0
L² 0.175 - 0.06206 L + 0.002 = 0
the equation remains after simplifying
L² - 0.3546 La + 0.01143 = 0
solve us
L =
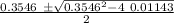
L =

L₁ = 0.319 m
L₂ = 0.036m
the correct result must have a value greater than the radius of the disk. The correct result is L = 0.319 m