Answer: Velocity of the ball just after the collision is -1.414 m/s.
Step-by-step explanation:
As energy is conserved in a reaction so here, energy before collision will be equal to the energy after collision.
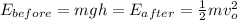
where,
m = mass
g = gravitational energy =
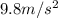
h = height or length
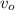 = initial velocity
= initial velocity
Also here, height is the length of wire. Let the height be denoted by 'L'. Therefore,
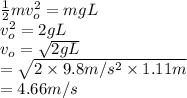
Formula used to calculate velocity after the collision is as follows.
![v_(f ball) = v_(o) [(m_(ball) - m_(block))/(m_(ball) + m_(block))]](https://img.qammunity.org/2022/formulas/physics/college/l15l1e29536jnd6gk9cji8rsjpsev2d3j1.png)
where,
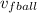 = final velocity of ball after collision
= final velocity of ball after collision
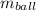 = masses of ball
= masses of ball
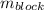 = masses of block
= masses of block
Substitute the values into above formula as follows.
![v_(f ball) = v_(o) [(m_(ball) - m_(block))/(m_(ball) + m_(block))]\\= 4.66 m/s [(1.48 kg - 2.77 kg)/(1.48 kg + 2.77 kg)]\\= 4.66 m/s * (-0.303)\\= -1.414 m/s](https://img.qammunity.org/2022/formulas/physics/college/sxcj4rzwitrbjf7ma1aunr2jv629jhjq8m.png)
Thus, we can conclude that velocity of the ball just after the collision is -1.414 m/s.