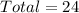Answer:
(a) 720 ways
(b) 120 ways
(c) 24 ways
Explanation:
Given

 --- number of letters
--- number of letters
Solving (a): Number of arrangements.
We have:

So, the number of arrangements is calculated as:
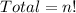
This gives:
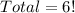
This gives:
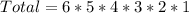
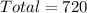
Solving (b): DA as a unit
DA as a unit implies that, we have:
[DA] N C E R
So, we have:
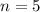
So, the number of arrangements is calculated as:
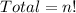
This gives:
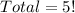
This gives:
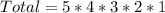
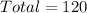
Solving (c): NCE as a unit
NCE as a unit implies that, we have:
D A [NCE] R
So, we have:

So, the number of arrangements is calculated as:
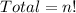
This gives:
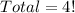
This gives: