This question is incomplete, the complete question is;
When light with a wavelength of 221 nm is incident on a certain metal surface, electrons are ejected with a maximum kinetic energy of 3.28 × 10⁻¹⁹ J. Determine the wavelength (in nm) of light that should be used to double the maximum kinetic energy of the electrons ejected from this surface.
Answer:
the required wavelength of light is 161.9 nm
Step-by-step explanation:
Given the data in the question;
Let us represent work function of the metal by W.
Now, using Einstein photoelectric effect equation;
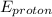 = W +
= W +
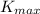
hc/λ = W +
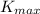 ------- let this be equation 1
------- let this be equation 1
we solve for W
W = hc/λ -
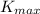
given that; λ = 221 nm = 2.21 × 10⁻⁷ m,
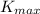 = 3.28 × 10⁻¹⁹ J
= 3.28 × 10⁻¹⁹ J
we know that speed of light c = 3 × 10⁸ m/s and Planck's constant h = 6.626 × 10⁻³⁴ Js.
so we substitute
W = [( (6.626 × 10⁻³⁴)(3 × 10⁸) )/2.21 × 10⁻⁷ ] - 3.28 × 10⁻¹⁹
W = 8.99457 × 10⁻¹⁹ - 3.28 × 10⁻¹⁹
W = 5.71457 × 10⁻¹⁹ J
Now, to determine λ for which maximum kinetic energy is double
so;
 = double = 2( 3.28 × 10⁻¹⁹ J ) = 6.56 × 10⁻¹⁹ J
= double = 2( 3.28 × 10⁻¹⁹ J ) = 6.56 × 10⁻¹⁹ J
from from equation 1
we solve for λ'
λ' = hc / W +

we substitute
λ' = ( (6.626 × 10⁻³⁴)(3 × 10⁸) ) / ( (5.71457 × 10⁻¹⁹ J) + ( 6.56 × 10⁻¹⁹ J ))
λ' = 1.9878 × 10⁻²⁴ / 1.227457 × 10⁻¹⁸
λ' = 1.619 × 10⁻⁷ m
λ' = 161.9 nm
Therefore, the required wavelength of light is 161.9 nm