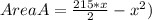Answer:
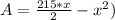
Explanation:
From the question we are told that:
Total length of building side
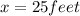
Perimeter of fence in
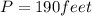
Generally the perimeter of the display area is given as mathematically given by
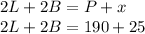
Therefore
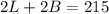
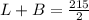
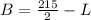
Generally the Area of the display area A is given as mathematically given by
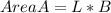
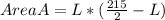
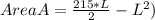
Length L in terms of x