Question

The Edward James Toy Company uses a Kanban system to make plastic wheels that are a component of several toys. The waiting time for a container of the wheels during production is 0.25 day; average processing time is 0.15 day per container. Each container holds 200 wheels. The company uses 2,000 wheels a day in the production of its products. Use the information in Case 6.1. Using a policy variable of 5%, calculate the number of Kanban containers needed for the wheels.

Answer 1

`N_c \approx 5.0`

Explanation:

From the question we are told that:

Waiting time for a container of the wheels during production
`T_w=0.25day`

Average processing time is
`T_a=0.15 day per container`

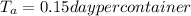
Wheel per container
`N_w=200`

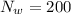
Total wheel per day
`D=2000`

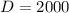
Policy variable of
`X=5%`

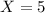
Generally the equation for Total number of container
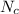`N_c` is mathematically given by

`N_c=DT((1+X)/(N_w) )`

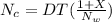
Where

Total time
`T=T_w+T_a`

`T=0.15+0.25`

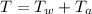
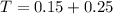
Therefore

`N_c=DT((1+X)/(N_w) )`

`N_c=2000*0.40((1+0.5)/(200) )`

`N_c=((840)/(200) )`

`N_c=4.2`

`N_c \approx 5.0`

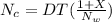
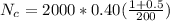
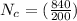
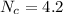
Therefore the number of Kanban containers needed for the wheels is

`N_c \approx 5.0`