Answer:
1) First of all we have to state the null hypothesis and also an alternative hypothesis.
Null hypothesis: ud< 0
Alternative hypothesis: ud > 0
It is important to note that these hypotheses are constituting a one-tailed test.
2) Second thing is to formulate an analysis plan. And for that, the significance level must be set to 0.05. And by Utilizing sample data, we will conduct a matched-pairs t-test of the null hypothesis.
3) Thirs thing is to analyze sample data. By utilizng the sample data, we calculate the following:
- standard deviation of the differences (s)
- standard error (SE) of the mean difference
- degrees of freedom (DF)
- t statistic test statistic (t).
s =
![sqrt [ (\sum (di - d)2 / (n - 1) ]](https://img.qammunity.org/2022/formulas/social-studies/college/og2r1vu43decuyt11bqmbe9w8vy761kaxe.png)
s = 0.55324
Standard error =
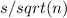
Standard error = 0.2259
Degree of freedom = n - 1 = 6 -1
DF = 5
t statistic test statistic (t). =
![[ (x1 - x2) - D ] / SE](https://img.qammunity.org/2022/formulas/social-studies/college/4ms1edg8dv8r20bsytpramo73ryb7lis1q.png)
t statistic test statistic (t). = 1.55
Here di shows observed difference for pair i
d shows the mean difference between sample pairs
D shows the hypothesized mean difference between population pairs
n shows the number of pairs.
Hence we now have a two-tailed test
the P-value is the probability that a t statistic having 5 degrees of freedom is more extreme than 1.55; i-e less than - 1.55 or greater than 1.55.
Hence, the P-value = 0.182
Now interpret the results. As we know the P-value (0.182) is > (0.05) the significance level , Null hypothesis is accpeted.
We cannot reject H0. Which means that we are lacking evidence at the 5% level that the mean count of T cells is higher after 20 days on blinatumomab.