Question

The standard gasoline engine for the 2017 Toyota Corolla includes the following data: Configuration: In-line four-stroke, four-cylinder engine Bore: 3.17 in Stroke: 3.48 in Compression ratio: 10.6:1 Assuming an ideal Otto cycle to describe this engine. Consider the working fluid to be air, modeled as an ideal gas with variable specific heat. Determine: (a) The total engine volume VBDC for all cylinders (cu.in). (b) The mass of air (lbm) contained in the engine assuming ambient conditions of 540 R and 14.7 psia. (c) The efficiency of the engine (%). The maximum temperature that occurs during the cycle is 3600 R.

Answer 1

a) The total engine volume is 30.3265 in³

b) the mass of air contained in the engine is 0.00129 lbm

c) The efficiency of the engine is 55.6%

Explanation:

Given the data in the question;

The configuration is in line with four-stroke, four-cylinder engine.

Bore ( d ) = 3.17 in

Stroke ( L ) = 3.48 in

compression ratio ( r ) = 10.6 : 1

First, we calculate the swept Volume V₁ = π/4 × d²L

we substitute

V₁ = π/4 × (3.17 )² × (3.48) = 27.4655 in³

Now, Compression Ration; r = Vs + Vc / Vc

r = (V₁ + V₂) / V₂

we substitute

10.6 = (27.4655 + V₂) / V₂

10.6V₂ = 27.4655 + V₂

10.6V₂ - V₂ = 27.4655

9.6V₂ = 27.4655

V₂ = 2.861 in³

So

a) total engine volume

`V_{BDC` = V₁ + V₂

we substitute

`V_{BDC` = 27.4655 in³ + 2.861 in³

`V_{BDC` = 27.4655 in³ + 2.861 in³

`V_{BDC` = 30.3265 in³

Therefore, The total engine volume is 30.3265 in³

b) The mass of air

given that; T = 540°R, P = 14.7 psia

we know that; PV = mRT { R is constant }

we solve for m

m = PV / RT

we substitute

m = (14.7 × 30.3265) / ( 0.3704 × 1728 )540

m = 445.79955 / 345627.648

m = 0.00129 lbm

Therefore, the mass of air contained in the engine is 0.00129 lbm

c) The efficiency

from table { properties of air}

At 540°R; u₁ = 92.04 BTu/lbm, u
`_r`₁ = 144.32

Now process 1 - 2 ( Isentropic ) u
`_r`₁ / u
`_r`₂ = V₁/V₁ = r

so, u
`_r`₁ / u
`_r`₂ = r

144.32 / u
`_r`₂ = 10.6

u
`_r`₂ = 144.32/10.6

u
`_r`₂ = 13.61

Thus, at u
`_r`₂ = 13.61, u₂ = 235 BTU/lbm, T₂ = 1340°R

Now, we know that;

P₁V₁/T₁ = P₂V₂/T₂ ⇒ (P₁/V₁)r = P₂/T₂

⇒ ( 14.7 / 540 )10.6 = P₂/1340

P₂ = 386.664 psia

process 2 - 3; constant volume heat addition;

Now, At T₃ = 3600°R, u₃ = 721.44 BTU/lbm, u
`_r`₃ = 0.6449

so,
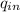`q_{in` = u₃ - u₂

we substitute

so,
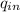`q_{in` = 721.44 - 235 = 486.44 BTU/lbm

Next, process 3 - 4; Isentropic

u
`_r`₄/u
`_r`₃ = V₄/V₃ = r

u
`_r`₄ / 0.6449 = 10.6

u
`_r`₄ = 6.8359

At u
`_r`₄ = 6.8359; u₄ = 308 BTU/lbm

∴

Heat Rejection
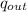`q_{out` = u₄ - u₁ = 308 - 92.04 = 215.96 BTU/lbm

so,
`W_{net` =
`q_{in` -
`q_{out`

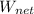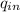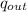
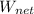`W_{net` = 486.44 - 215.96

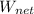`W_{net` = 270.48 BTU/lbm

so the efficiency; η
`_{thermal` = (
`W_{net` /
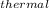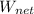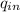`q_{in` ) × 100%

η
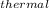`_{thermal` = ( 270.48 / 486.44 ) × 100%

η
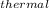`_{thermal` = ( 0.55604 ) × 100%

η
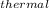`_{thermal` = 55.6%

Therefore, The efficiency of the engine is 55.6%