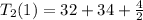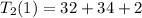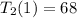Answer:
68 meters moved in the next seconds
Step-by-step explanation:
Given
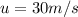
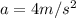
Required
Distance covered by the car in the next second
At a point in time t, the current distance is calculated as:

Substitute values for a and u in the above equation.
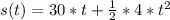
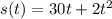
Next, we generate the second degree Taylor polynomial as follows;
Calculate velocity (s'(t))
Differentiate s(t) to get velocity
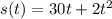

Calculate acceleration (s"(t))
Differentiate s'(t) to get acceleration

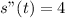
When t = 0
We have:

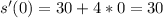
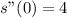
So, the second degree tailor series is:
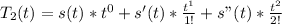
To see the distance moved in the next second, we set t to 1
So, we have:

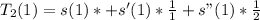
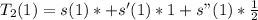
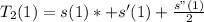
Solving s(1), s'(1) and s"(1)
We have:
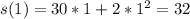
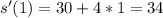
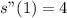
Hence: