Answer:
The ratio of the drag coefficients
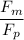 is approximately 0.0002
is approximately 0.0002
Explanation:
The given Reynolds number of the model = The Reynolds number of the prototype
The drag coefficient of the model,
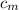 = The drag coefficient of the prototype,
= The drag coefficient of the prototype,
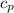
The medium of the test for the model,
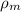 = The medium of the test for the prototype,
= The medium of the test for the prototype,
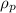
The drag force is given as follows;
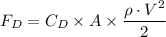
We have;
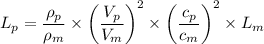
Therefore;
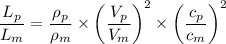
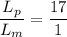

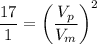
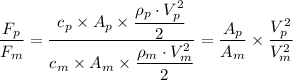
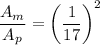
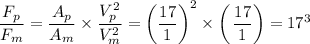
 = (1/17)^3 ≈ 0.0002
= (1/17)^3 ≈ 0.0002
The ratio of the drag coefficients
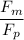 ≈ 0.0002.
≈ 0.0002.