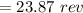Question

A wheel rotates about a fixed axis with an initial angular velocity of 20 rad/s. During a 5.0-s interval the angular velocity increases to 40 rad/s. Assume that the angular acceleration was constant during the 5.0-s interval. How many revolutions does the wheel turn through during the 5.0-s interval ( in revelations)? Hint: You need to use one of the equations of constant angular acceleration that independent of angular acceleration.

Answer 1

The appropriate solution is "23.87 rev".

Step-by-step explanation:

The given values are:

Initial angular velocity,

`\omega_i=20 \ rad/s`

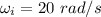
Final angular velocity,

`\omega_f=40 \ rad/s`

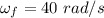
Time taken,

`t = 5.0 \ s`

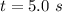
If, α be the angular acceleration, then

⇒
`\omega_f=\omega_i+\alpha t`

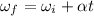
or,

⇒
`\alpha t=\omega_f-\omega_i`

⇒
`\alpha=(\omega_f-\omega_i)/(t)`

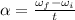
On substituting the values, we get

⇒
`=(40-20)/(5.0)`

⇒
`=(20)/(5.0)`

⇒
`=4 \ rad/s^2`

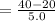
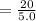
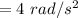
If, ΔФ be the angular displacement, then

⇒
`\Delta \theta=\omega_i t+(1)/(2) \alpha t^2`

On substituting the values, we get

⇒
`=[(20* 5.0)+((1)/(2))* 4* (5.0)^2]`

⇒
`=100+50`

⇒
`=150`

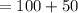
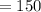
On converting it into "rev", we get

⇒
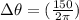
`\Delta \theta=((150)/(2 \pi) )`

⇒
`=23.87 \ rev`