Question

a ball rolls horizontally of the edge of the cliff at 4 m/s, if the ball lands at a distance of 30 m from the base of the vertical cliff, what is the the hight of the cliff

Answer 1

Approximately
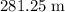`281.25\; \rm m`. (Assuming that the drag on this ball is negligible, and that
`g = 10\; \rm m \cdot s^(-2)`.)

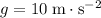Step-by-step explanation:

Assume that the drag (air friction) on this ball is negligible. Motion of this ball during the descent:

• Horizontal: no acceleration, velocity is constant (at
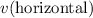  `v(\text{horizontal})` is constant throughout the descent.)
• Vertical: constant downward acceleration at
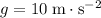  `g = 10\; \rm m \cdot s^(-2)`, starting at
  `0\; \rm m \cdot s^(-1)`.

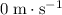The horizontal velocity of this ball is constant during the descent. The horizontal distance that the ball has travelled during the descent is also given:
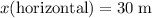`x(\text{horizontal}) = 30\; \rm m`. Combine these two quantities to find the duration of this descent:

`\begin{aligned}t &= \frac{x(\text{horizontal})}{v(\text{horizontal})} \\ &= (30\; \rm m)/(4\; \rm m \cdot s^(-1)) = 7.5\; \rm s\end{aligned}`.

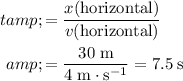In other words, the ball in this question start at a vertical velocity of
`u = 0\; \rm m \cdot s^(-1)`, accelerated downwards at
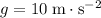`g = 10\; \rm m \cdot s^(-2)`, and reached the ground after
`t = 7.5\; \rm s`.

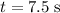Apply the SUVAT equation
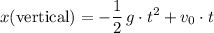`\displaystyle x(\text{vertical}) = -(1)/(2)\, g \cdot t^(2) + v_0\cdot t` to find the vertical displacement of this ball.

`\begin{aligned}& x(\text{vertical}) \\[0.5em] &= -(1)/(2)\, g \cdot t^(2) + v_0\cdot t\\[0.5em] &= - (1)/(2) * 10\; \rm m \cdot s^(-2) * (7.5\; \rm s)^(2) \\ & \quad \quad + 0\; \rm m \cdot s^(-1) * 7.5\; s \\[0.5em] &= -281.25\; \rm m\end{aligned}`.

In other words, the ball is
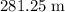`281.25\; \rm m` below where it was before the descent (hence the negative sign in front of the number.) The height of this cliff would be
`281.25\; \rm m\!`.