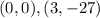1 Answer

Bryanbcook · Answer 1 · 2022-07-18T12:45:50+0000

Answer:
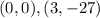
(0,0), (3,-27)

Explanation:

Given

Curve is
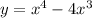
y=x^4-4x^3

The stationary point on a differentiable function is the points where the differentiation of the function is zero i.e. slope is zero at that point.

Differentiate the curve
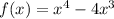
f(x)=x^4-4x^3

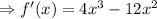
$\Rightarrow f'(x)=4x^3-12x^2$

Equate it to zero

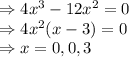
$\Rightarrow 4x^3-12x^2=0\\\Rightarrow 4x^2(x-3)=0\\\Rightarrow x=0,0,3$

Put
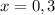x=0,3 in the function
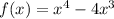
f(x)=x^4-4x^3

$\Rightarrow f(0)=0\\\Rightarrow f(3)=3^4-4(3)^3\\\Rightarrow f(3)=81-108\\\Rightarrow f(3)=-27$

Therefore, the stationary points are
(0,0), (3,-27)

Please log in or register to add a comment.