Question

Find the following trigonometric Fourier Series:

Answer 1

(a) Extend the definition of f(x) to make it an even function f*(x),

`f^*(x)=\begin{cases}0&\text{if }-2\le x<-1\\1&\text{if }0\le x\le1\\0&\text{if }1<x\le2\end{cases}`

and we take f* to be periodic over an interval of length P = 4. We compute the coefficients of the cosine series:

`a_n = \displaystyle\frac2P \int_(-2)^2 f^*(x)\cos\left(\frac{2n\pi}Px\right)\,\mathrm dx = \frac{2\sin\left(\frac{n\pi}2\right)}{n\pi}`

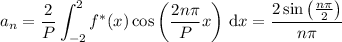
Note that a₀ = 1 (you can compute the integral again without the cosine, or just take the limit as n -> 0). For all other even integers n, the numerator vanishes, so we split off the odd case for n = 2k - 1 :

`a_(2k-1) = \frac{2\sin\left(\frac{(2k-1)\pi}2\right)}{(2k-1)\pi}`

Then the cosine series of f(x) is

`\displaystyle \frac{a_0}2 + \sum_(k=1)^\infty a_(2k-1)\cos\left(\frac{(2k-1)\pi}2x\right)`

(b) For the sine series, you instead extend f(x) to an odd function f*(x),

`f^*(x)=\begin{cases}-1&\text{if }-2\le x\le-1\\x&\text{if }-1<x<1\\1&\text{if }1\le x\le2\end{cases}`

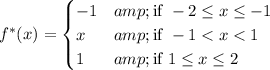
Again, P = 4, and the coefficient of the sine series are given by

`b_n = \displaystyle\frac2P\int_(-2)^2f^*(x)\sin\left(\frac{2n\pi}Px\right)\,\mathrm dx`

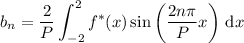
which we can again split into the even/odd cases,

`b_(2k) = -\frac1{k\pi}`

`b_(2k-1) = (4(-1)^(k+1)+2(2k-1)\pi)/((2k-1)^2\pi^2)`

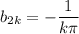
So the sine series is

`\displaystyle \sum_(k=1)^\infty\left(b_(2k)\sin\left(k\pi x\right) + b_(2k-1)\sin\left(\frac{(2k-1)\pi}2x\right)\right)`

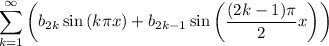
I've attached plots of the extended versions of f(x) along with the corresponding series up to degree 4.