Question

Help ASAP with working if possible ​

Answer 1

1. The volume of the cylinder is approximately 0.153 m³

2. 25 cm

3.
`25.\overline 6 \ cm`

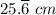
4. 16 m

5. 1,785 m³

Explanation:

The volume of a solid can be found by the product of the uniform cross-sectional area of the solid and the (continuous) length of the solid

1. The uniform cross-sectional area of the given cylinder = The area of the circle at the base or top

The dimension of the diameter of the circle at the top of the cylinder, d = 50 cm = 0.5 m

The area of the circular cross-section, A = π·d²/4

∴ A = π × 0.5²/4 = 0.0625·π

A = 0.0625·π m²

The height of the cylinder, h = The continuous length of the circular cross-section = 78 cm = 0.78 m

∴ The volume of the cylinder, V = A × h

∴ V = 0.0625·π × 0.78 = 0.04875·π ≈ 0.153

The volume of the cylinder, V ≈ 0.153 m³

2. The given volume of the trapezium, V = 8550 cm³

The length of the short and long parallel sides 'a', and 'b', are 17 cm and 21 cm respectively

The height of the trapezium from the diagram, h = 18 cm

The cross-sectional area of the trapezium, 'A', is found as follows;

A = (17 cm + 21 cm)/2 × 18 cm = 342 cm²

The volume of the trapezium, V = The cross-sectional, A × The (missing) length, 'l' of the trapezium

∴ l = V/A

By substitution, we have;

l = 8550 cm³/(342 cm²) = 25 cm

∴ The Missing Length, l = 25 cm

3. The given volume of the solid having a uniform cross-sectional area is, V = 385 cm³

The area of the (uniform) cross-section of the solid, A = 15 cm²

∴ The length of the solid, 'l', from V = A × l, is given as follows;

l = V/A

∴ l = 385 cm³/(15 cm²) = 25.
`\overline 6` cm

The length of the solid, l = 25.
`\overline 6` cm

4. From the diagram, we have;

The cross-sectional area of the solid, A = 216 m²

The length of the solid, l = 16 m

5. The cross-section of the solid can can be assumed to be either;

1. A trapezium from which a rectangle has been removed of dimensions 8 m by 9 m.

2. A triangle located above a rectangle

For scenario one, we have;

The cross-sectional area, A = (12.5 + 9)/2 × 15 - 8 × 9 = 89.25

For scenario two, we find 'A' as follows;

A = 7 × 9 + 1/2 × 15 × 3.5 = 89.25

∴ The cross-sectional area of the solid, A = 89.25 m²

The length, 'l', of the solid, is given as l = 20 m

The volume of the solid, V = A × l

∴ V = 89.25 m² × 20 m = 1,785 m³

The volume of the solid, V = 1,785 m³.