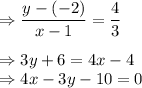Question

A) Find the slope, x-intercept, y-intercept of the line (L):

3x+4y-6= 0 and draw its graphs.
b) Find the equation of a line perpendicular to the line (L) in part (a) and
passing through the point (1, -2).​

Answer 1

Answer: 2, 1.5 , -0.75

(b)
`4x-3y-10=0`

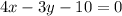
Explanation:

Given

line is
`3x+4y-6=0`

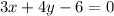
Converting it into intercept form

`\Rightarrow 3x+4y=6\\\\\Rightarrow (3x)/(6)+(4y)/(6)=(6)/(6)\\\\\Rightarrow (x)/(2)+(y)/(1.5)=1`

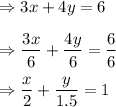
So, the x-intercept is
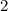`2` and y-intercept is
`1.5`

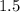
The slope is given by

`-((1)/(2))/((1)/(1.5))=-0.75`

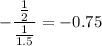
(b) the line perpendicular to the above line and passing through
`(1,-2)`

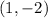
The slope of the required line

`m=-(1)/(-0.75)\\\\m=(4)/(3)`

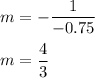
Equation of the line is given by

`\Rightarrow (y-(-2))/(x-1)=(4)/(3)\\\\\Rightarrow 3y+6=4x-4\\\Rightarrow 4x-3y-10=0`