Question

A lorry is travelling at 13.5m/s along a stretch of road​

Answer 1

Proved

Explanation:

This question is incomplete. The complete details are:

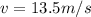`v = 13.5m/s` --- speed of the lorry

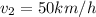`v_2 =50km/h` --- speed limit on the road

Required

Prove that the lorry is within the speed limit

To do this, we simply convert the speed of the lorry to km/h.

So, we have:

`v = 13.5m/s`

`1m = 0.001km`

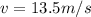
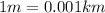
and

`1s = (1)/(3600)h`

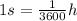
So, the expression becomes:

`v = (13.5 * 0.001km)/(1/3600h)`

`v = (0.0135km)/(1/3600h)`

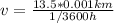
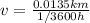
Rewrite as:

`v = 0.0135km/h * 3600`

`v = 48.6km/h`

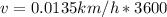
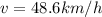
48.6km/h is less than 50km/h (the speed limit).

Hence, the lorry is within the speed limit.