Question

The function y=60+25sin(pi/6)t, where t is in months and t=0 corresponds to April 15, models the average high temperature in degrees Fahrenheit in Centerville.

b.) What is the maximum high temperature and when does this occur?

NOTE: I found the answer online, I just don't understand how to get there. It's July 15, 85 degrees.

Answer 1

The maximum temperature will be of 85 degrees, on July 15.

Explanation:

Sine function:

The sine function oscilates between -1 and 1, and it's maximum value is:

`\sin{((\pi)/(2))} = 1`

y=60+25sin(pi/6)t

The maximum value will occur when
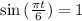`\sin{((\pi t)/(6)}) = 1`, and it will be of 60 + 25 = 85 degrees.

When will it occur?

First we find the value of t for which the value inside the function sine is
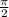`(\pi)/(2)`. So

`(\pi t)/(6) = (\pi)/(2)`

`(t)/(6) = (1)/(2)`

`2t = 6`

`t = (6)/(2) = 3`

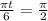
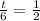
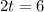
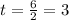
That is the number of months after April 15, which is 3 months. So July 15.