The measure of angle A. is approximately
 when rounded to two decimal places.
when rounded to two decimal places.
In a right-angled triangle ABC where angle ABC is 90 degrees, and sides AC and AB are given as 32 m and 49 m, respectively, we can use trigonometry to find the measure of angle A.
The tangent of an angle in a right-angled triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
![\[ \tan(A) = \frac{{\text{opposite side}}}{{\text{adjacent side}}} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/vsoj5phhez114u1l2q6dajyu3wh0pkblkf.png)
In this case,
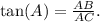
Using the inverse tangent function
 on a calculator, we find:
on a calculator, we find:
![\[ A = \tan^(-1)\left(\frac{{49}}{{32}}\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/clljqeyjqaabb6bwilzg0ujpg3is4de36d.png)
Let's calculate
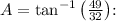
![\[ A = \tan^(-1)\left(\frac{{49}}{{32}}\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/clljqeyjqaabb6bwilzg0ujpg3is4de36d.png)
Using a calculator:
![\[ A \approx \tan^(-1)\left(1.53125\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/m8x6t52tqjbxmpgsxm4cf9112buoqjgbg9.png)
![\[ A \approx 56.31^\circ \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ao4dqct1vl1ac5ca0jy2cd9yjnqk00kecf.png)
Therefore, measure of angle A. is approximately
 when rounded to two decimal places.
when rounded to two decimal places.
The probable question may be:
In triangle ABC, angle ABC=90 degree, AC=32 m, AB=49 m
Use the inverse trigonometric keys on a calculator to find the measure of angle A. A=_____° (Round the answer to the nearest whole number.)