Question

A certain television is advertised as a 90- inch Tv ( the diagonal length).

Answer 1

The width is 64.3 inches

Explanation:

Given

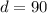`d = 90` --- diagonal

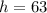`h = 63` --- height

Required

Determine the width (w) of the TV

To do this, we make use of Pythagoras theorem which is illustrated as:

`d^2 = h^2 + w^2`

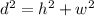
So, we have:

`90^2 = 63^2 + w^2`

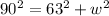
Evaluate all squares

`8100 = 3969 + w^2`

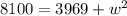
Collect like terms

`w^2 = 8100 - 3969`

`w^2 = 4131`

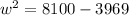
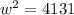
Take positive square roots of both sides

`w = \sqrt{4131`

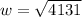
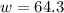`w = 64.3` -- approximated