Question

Which equation shows the quadratic formula used correctly to solve 7x^2 = 9 + x for x?

Answer 1

Explanation:

We must rewrite 7x^2 = 9 + x in standard form first: 7x^2 - x - 9 = 0.

The coefficients are 7, -1 and -9, and so the discriminant b^2 - 4ac is

(1)^2 - 4(7)(-9) = 253.

The roots are:

-(-1) ± √253 1 ± √253

x = --------------------- = --------------------

2(7) 14

Answer 2

The correct quadratic formula to solve
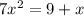`\(7x^2 = 9 + x\)` is
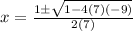`\(x = (1 \pm √(1 - 4(7)(-9)))/(2(7))\)`. The accurate representation is given in option B.

The correct quadratic formula for solving
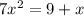`\(7x^2 = 9 + x\)` is represented as follows:

`\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]`

Comparing this with the provided options:

A. Incorrect. The term inside the square root is incorrect; it should be
`\(9 - 4(7)(1)\)`.

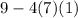B. Correct. The quadratic formula is used correctly with the correct values for a, b, and c.

C. Incorrect. The term inside the square root is incorrect; it should be
`\((-1)^2 - 4(7)(9)\)`.

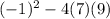D. Incorrect. The term inside the square root is incorrect; it should be
`\((-1)^2 - 4(7)(9)\)`.

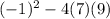Therefore, the correct answer is B:

`\[ x = (1 \pm √((-1)^2 - 4(7)(9)))/(2(7)) \]`